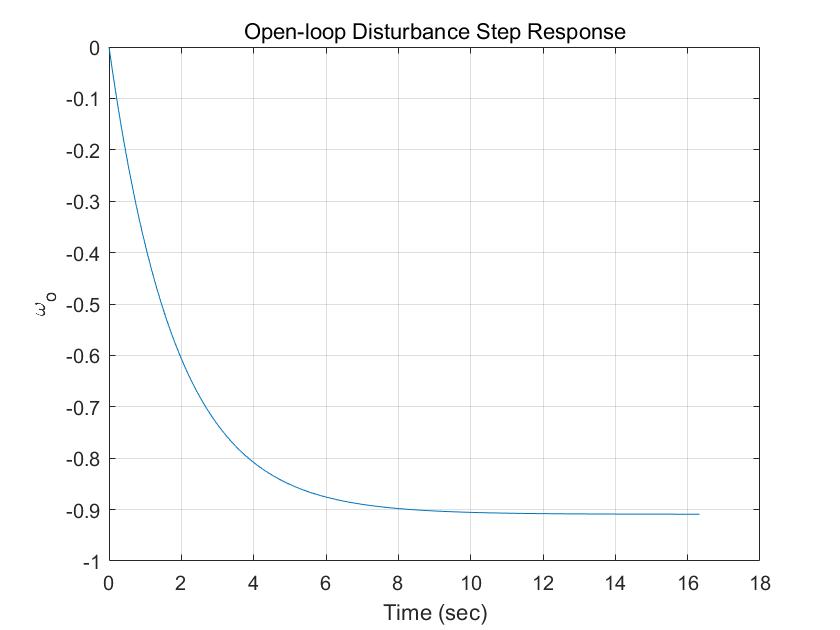
第二章 模型评估与选择
经验误差与过拟合:
样本误差,测试误差,泛化误差
过拟合:将训练样本本身的特点当作所有样本的一般性质,导致泛化性能下降
目前的解决方法:优化目标加正则项、early stop
评估方法:
我们假设测试集是从样本真实分布中独立采样获得,将测试集上的测试误差作为泛化误差的近似,所以测试集和训练集要尽可能的互斥。
通常将m个样本的数据集D,拆分成训练集S和测试集T
1.留出法 直接将数据集划分为两个互斥集合,测试/训练集的数据分布要尽量保持一致。一般做若干次随机划分,重复实验取平均值
2.交叉验证法
将数据集划分成k个大小相同的互斥子集。每次用k-1个子集的并集作为训练集,余下的子集作为测试集,最终返回k个测试结果的均值。
留一法:交叉验证的特例。m个样本只有唯一方法划分为m个子集——每个子集包含一个样本。
3.自助法
每次在D里选一个样本,放到D‘,然后放回。重复执行m次,获得一个D’。
性能量度:
错误率和精度:加起来等于1 。错误率就是错的占样本的比例,精度就是对的占样本的比例。
混淆矩阵:TP(真正例)+FP(假正例)+TN(真反例)+FN(假反例)=样例总数
查准率和查全率:P=TP/(TP+FP)查准率 R=TP/(TP+FN)查全率
以查准率为Y轴查全率为X轴,做P-R曲线。哪个包住了哪一个就是效果更好。在两个曲线有交叉的情况下,可以计算面积。或者考虑在某一个特定的点下,查准率和查全率的指标。
“平衡点”:平衡点是曲线上查询率=查全率时的取值。平衡点谁更高。哪个学习器就更好。
F1度量:F1=(2xTP)/(样例总数+TP-TN) \[
F_{\beta}=\frac{(1+\beta^2)\times P \times R}{(\beta^2\times P)+R}
\] ROC与AUC:很多学习器的测试样本产生一个实值或者概率预测,然后将这个预测值和一个分类阈值进行比较,大于则为正例,小于则为反例。ROC曲线的纵轴是真正例率(TPR True Positive Rate),横轴是假正例率(FPR false Positive Rate)。
AUC值是ROC曲线下的面积,即Area Under ROC Curve。根据ROC的画法,AUC的计算可以估算为矩形面积: \[
AUC=\frac{1}{2}\sum^{m-1}_{i=1}(x_{i+1}-x_i).(y_i+y_{i+1})
\]
比较检验:
假设检验:假设检验中的“假设”是对学习器泛化错误率分布的某种判断或猜想。例如a<a0。我们可以使用二项检验或者t检验。
交叉验证t检验,5x2交叉验证是做五次2折交叉验证。
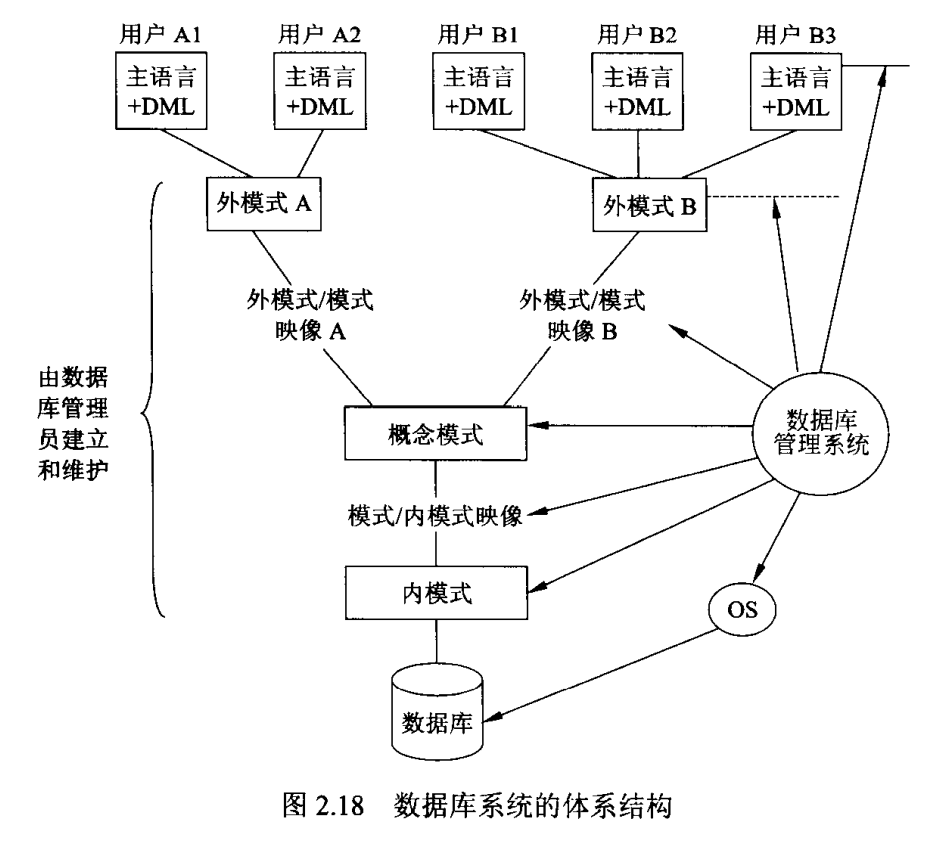 数据库系统中数据的三级模式结构
数据库系统中数据的三级模式结构
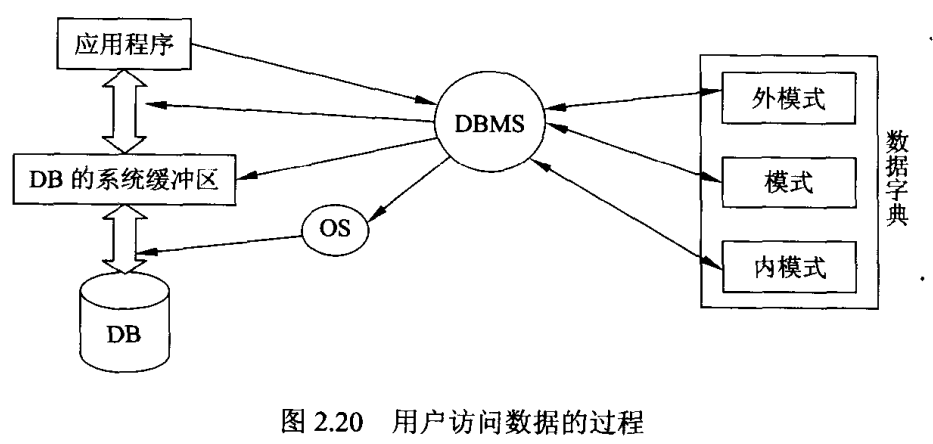 用户访问数据的过程
用户访问数据的过程
 猫猫
猫猫
 好像是早上
好像是早上
 某个小朋友想养的萨摩耶
某个小朋友想养的萨摩耶